François-René Rideau

Reflection with First-Class Implementations

François-René Rideau F.3.2 Semantics of Programming Languages First-class implementations, Reflection, Software Architecture

We propose an approach to reconcile formal methods and computational reflection. First, we introduce a formalism to study implementations, with which we express some of their desirable properties, notably one we dub observability. Next, we derive a protocol for first-class implementations, that enables zooming up and down the abstraction levels of a computation at runtime. Then we show how this unifies discussion of previously disparate techniques (from static analysis to AOP) and even trivializes some difficult ones (like live code migration). Finally, we envision how our proposed first-class semantic virtualization enables a new software architecture.

1 Introduction

1.1 Category Theory

We use Category Theory to formalize computation, but only in elementary ways that require no prior knowledge of it. Here is a summary of the concepts used in this article.

A category (a) contains a set Node of nodes (or objects), and for any pair of nodes x, y a set Arrow x y of arrows (or morphisms) connecting x to y, (b) is closed under composition of arrows, whereby given nodes x, y, z : Node and arrows f : Arrow x y and g : Arrow y z, there is an arrow g ∘ f : Arrow x z, and (c) contains for every node x an arrow identity x : Arrow x x, that is neutral for composition left or right.

A functor maps the nodes and arrows of one category to those of another, preserving the composition structure of arrows (and any additional structure, if applicable). A category B is a subcategory of A if B’s nodes and arrows are subsets of A’s, respectively. B is said to be a full subcategory if for any x, y in B.Node (and thus also in A.Node), B.Arrow x y = A.Arrow x y.

2 Implementations

2.1 Computations as Categories

We consider a computation as a category in which nodes are the potential states of the computation and arrows are the transitions between those states; arrows between the same nodes are distinguished by their side-effects if any. This approach has two advantages: (1) it unifies a wide range of popular formalisms, including operational semantics, labeled transition systems, term rewriting, modal logic, partial orders, etc.; (2) by using the versatile mathematical tool that is category theory, we get many structural theorems “for free”, including the ability to extract programs from proofs using the Curry-Howard correspondance.

An interpretation of a concrete computation $C$ as an abstract computation $A$ is a partial functor Φ from $C$ to $A$. Its inverse is called an implementation of $A$ with $C$; it is a non-deterministic partial injective profunctor. Interpretations are the morphisms of a category of computations; implementations are the morphisms of its dual category.

Partiality expresses the fact that most computation states and transitions are intermediate states with no direct meaning in the abstract computation, as in the proverbial non-atomic transfer of resources between two owners; only observable concrete states can be interpreted as having an abstract meaning. Partiality allows discrete computations to be implemented with continuous computations, infinite ones with finite ones, the non-deterministic with the deterministic, etc., and vice-versa. Now, category theory is usually presented in terms of total functions, so we define a partial functor Φ from $C$ to $A$ as the data of (1) a full subcategory $O$ of the observable states of $C$, and (2) a (total) functor $\phi : O \rightarrow A$.

In general the nodes of a computation encode dynamic execution state such as registers, bindings, mutable store, call stacks, messages sent and received, etc. An implementation is injective; it must distinguish the states it implements, and cannot lose that information, though it can add implementation details and drop alternatives not taken. Conversely, interpretations may lose information, introduce approximations, or add alternatives — and indeed include static analysis, type systems and abstract interpretation, that do.

2.2 Properties of Implementations

Soundness		Totality		Completeness

Bounded Liveness		Observability

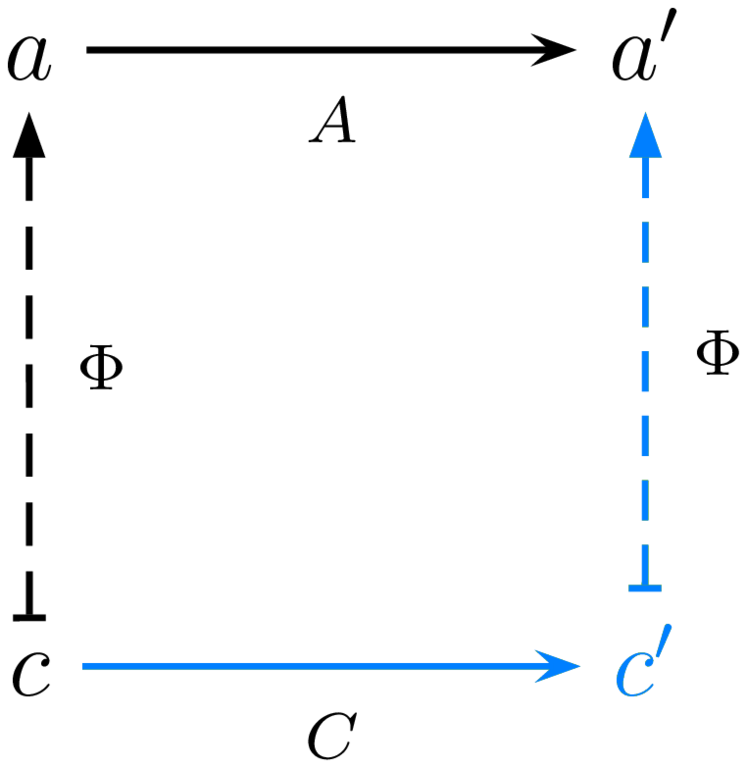
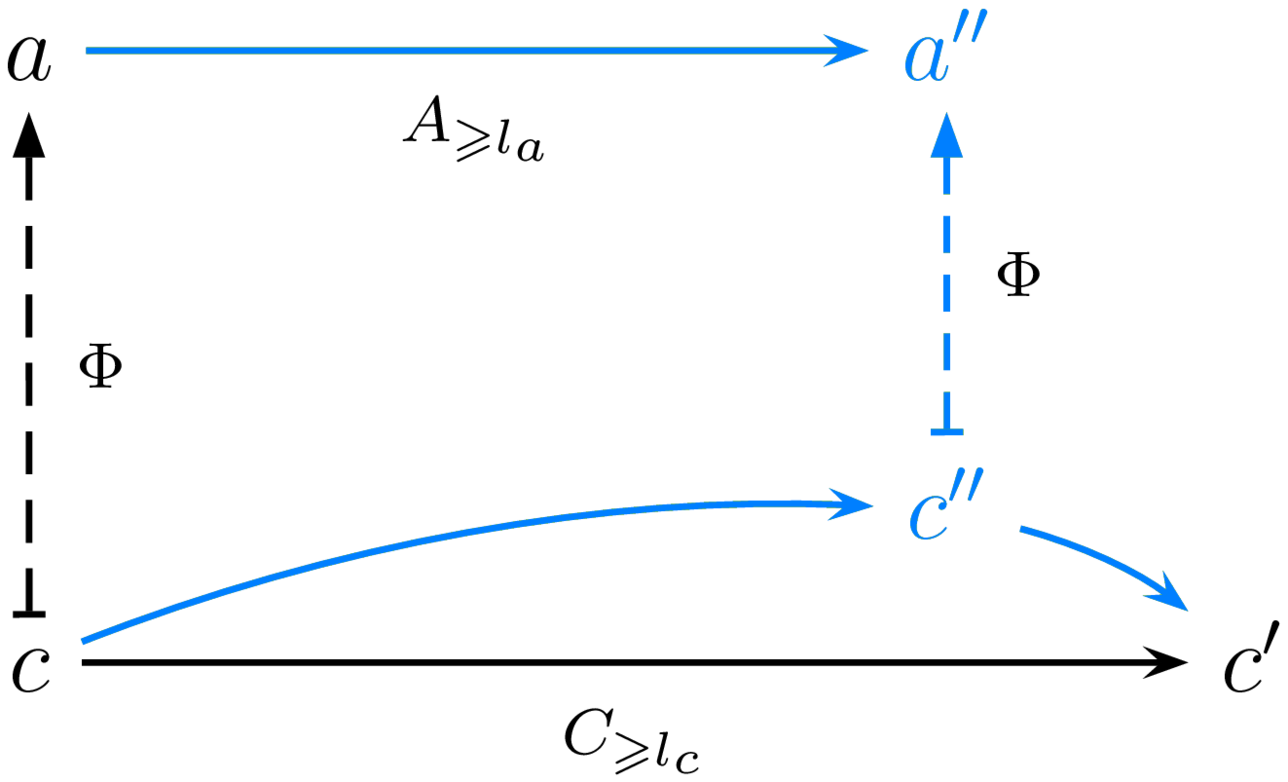
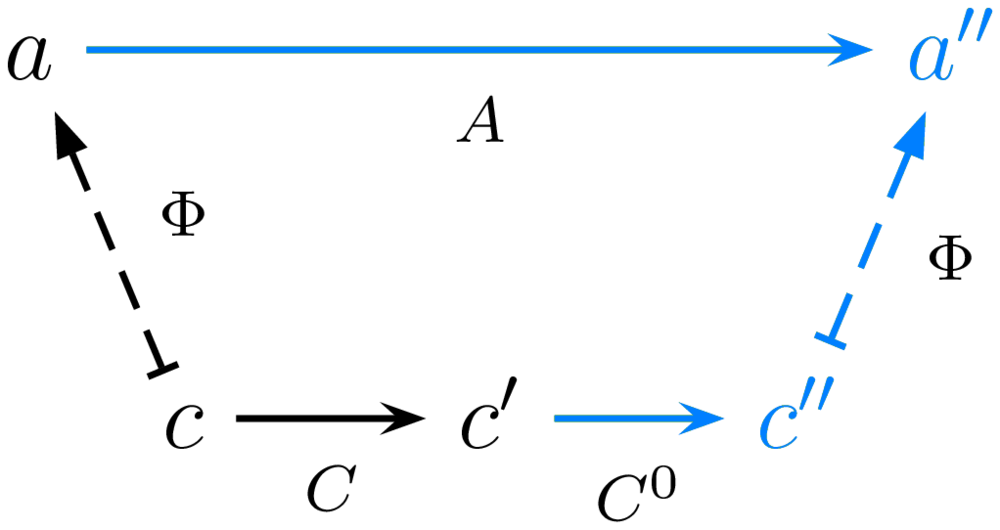
Figure 1: A few properties that any given implementation may or may not possess

We identify several common desirable properties for implementations to possess. We outlined elsewhere how to formalize them in Agda, together with many variants; but we like to illustrate the simpler properties as in Figure 1. In these diagrams: (a) horizontal arrows are arrows in a computation (morphism of the category), with evaluation time running from left to right; (b) vertical arrows are interpretation arrows, pointing up, with abstract system on top and concrete system at the bottom; note that in the above diagrams these vertical arrows are associations rather than function declarations; also note that implementation arrows would be pointing down, but we show interpretation arrows instead because they are functorial, i.e. preserve structure; (c) the diagrams commute, i.e. any two ways to follow arrows from a node to another lead to equality of the composed arrows; (d) in black are the hypotheses of the property, in blue are its conclusions (assuming the property holds).

The most basic property is soundness: if the concrete implementation includes a transition $g$ from $c$ to $c'$ and $c$ is observable with interpretation $a$ while and $c'$ is observable with interpretation $a'$, then there is a valid transition $f$ from $a$ to $a'$ such that $\Phi(g) = f$. In other words, if an (intermediate or final) answer is reached using the concrete computation, the answer must be correct in the abstract computation. This property is so fundamental that it is actually implied by our construction of interpretations as a partial functor.

Many other properties are not as ubiquitous, but still desirable. For instance, totality (NB: of the implementation, from nodes, i.e. node-surjectivity of the interpretation) means that given an abstract state $a$ you can find a concrete state $c$ that implements it. Implementations need not be total (and obviously cannot be when implementing an infinite computation using a finite computer). However, when composing many layers of implementations, it is good if non-totality (or failure to satisfy whichever other property) can be restricted to a single layer, or a few well-identified layers (e.g. from running out of memory, or from exploring only a subset of possible choices in case of non-determinism or I/O, etc.).

Completeness enables the high-level user to arbitrarily influence low-level evaluation. In labeled transition systems, it means the implementation matches the usual notion of a simulation. It is essential for debugging, but has many other uses; notably, observability below is not composable, but the conjunction of observability and completeness is.

There are many variants of liveness, the property says that for “long enough” runs of the concrete computation, the abstract computation will have advanced “some”. One constructive variant, bounded liveness, assumes some additive metric for each of the abstract and concrete computations, and states that runs above a minimum length $l_c$ in the concrete computation, though they may not reach an observable state, must run “past” an observable state that can be interpreted as a run above a minimum length $l_a$ in the abstract computation.

Now, our biggest contribution is the notion of observability, that allows to retrieve an abstract computation state from an arbitrary concrete computation state, by first synchronizing to an observable state through a narrow enough subset $C^0$ of $C$ (that e.g. does not involve blocking on I/O or spending more than a fixed amount of some resources). Indeed, when a concrete computation is interrupted, it will in general be in an intermediate state that is not observable and cannot be interpreted as having an abstract meaning: it may be in the middle of a transaction; it may comprise the state of multiple threads none of which is in an observable state; the probability of any reachable state being observable may be negligible, or even be absolutely zero. Even if the compiler kept a trace of the interpretation function through which its correctness could be proven, there could be no observable state to which to apply it... unless the implementation has observability; then it is just a matter of using the property to extract an abstract state $a''$ from the state $c'$ of an interrupted concrete computation. Observability generalizes PCLSRing  (Bawden 1989), as well as many ad-hoc techniques used to implement garbage collection or database transactions.

3 First-Class Implementations

3.1 Protocol Extraction

We can write specifications for our properties with dependent types, and constructive proofs of the properties will have a useful computational content. By erasing type dependencies, implicit arguments and compile-time values, we can also get a less precise type suitable for use in run-of-the-mill typed programming languages.

By applying this extraction strategy systematically, we obtain a protocol to deal with implementations as first-class objects, where each property defines a trait for typeclasses of implementations, and suitable typeclasses define categories of computations and implementations. Actually, we obtain two protocols: in the first, reified protocol, nodes and arrows of the computations remain first-class objects and “running” the computation is a matter of formal reasoning, with any side-effects being representations; in the second, reflective protocol, the concrete computation is the “current” ambient computation, and running it causes side-effects to “actually” happen (as far as the metaprogram manipulating the represented computation is concerned). The key functions to switch between these two protocols are perform.node: Node → State and perform.arrow: Arrow → State → Effect State where State is the “actual” machine state and Effect its “actual” effect monad — and their “inverses” record.node: State → Node and record.arrow: State → (State → Effect State) → Effect Arrow. The reflective protocol enables navigation up and down a computation’s semantic tower — while it is running.

3.2 The Semantic Tower

Composition		Compilation		Static analysis

Figure 2: A few ways to think about implementations

Modeling computations as first-class categories can shed a new light on familiar activities.

Implementations can be composed and decomposed: thus, complex implementations can be broken down into many simple passes of compilation; languages can be implemented by composing a layer on top of previous ones; and instrumentation or virtualization can be achieved by composing new layers at the bottom. Computations are thus part of a semantic tower, made of all the layers composed between the abstract computation specified by the user and the underlying hardware (or physical universe). See Figure 2.

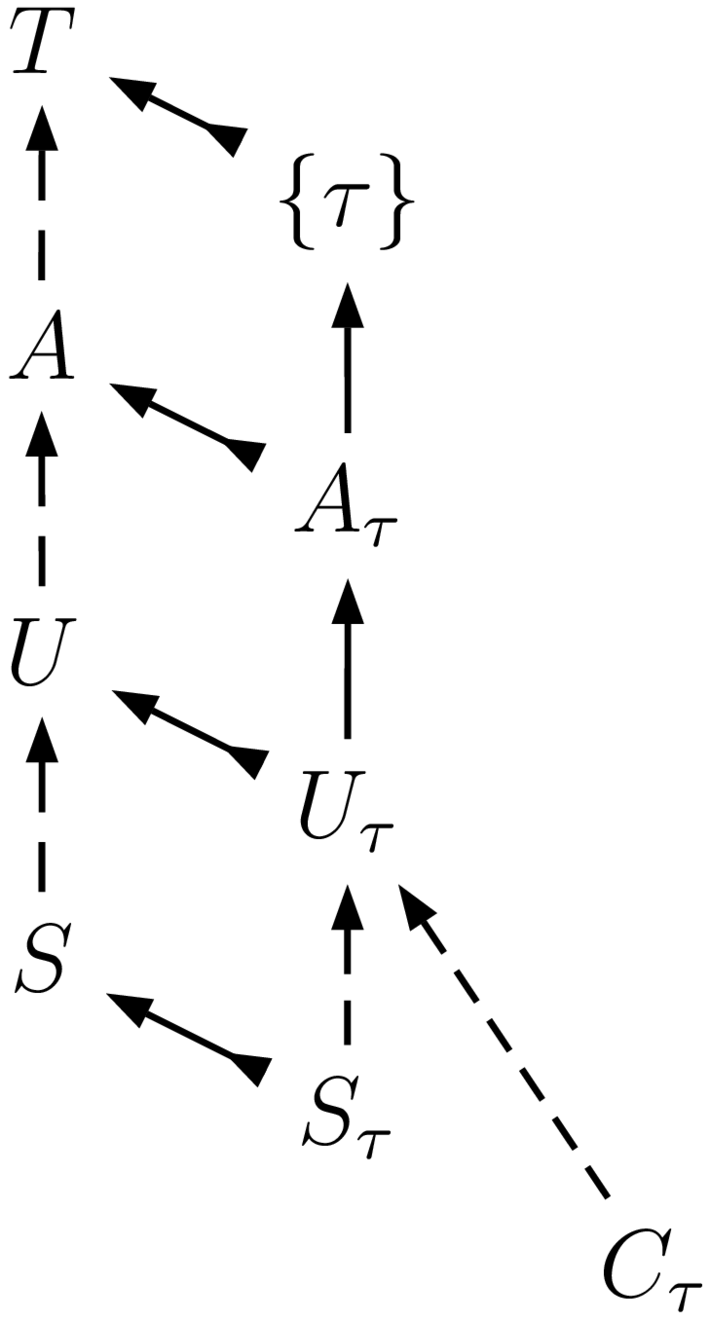
A naïve user could view a compiler as implementing his user-provided source code being an abstract computation $A$ with some object code $C$. But the source code $S$ is only a representation of the actual abstract computation $A$ desired by the user; this computation is defined up to an equivalence class, so an optimizing compiler can rewrite it into any of the equivalent computations. However, the equivalence class $A$ is not computable, whereas the model $U$ of equivalences understood by the compiler is; between the two is thus an irreducible semantic gap that algorithms can never fill. Now add static analysis to the picture: some source program can be proven to be in a subset where all nodes have static type $\tau$; therefore better specialized variants $A_\tau$, $U_\tau$ and $C_\tau$ can be used.

Many other topics can be reviewed in this light. Tweaking optimizations is about modifying $U$ in the above model. Refactoring is changing $S$ while keeping $U$ constant. Developing is modifying $A$ as being the user’s desired approximation of the trivial abstract computation $\top$ on top of all semantic towers. Aspect-oriented programming becomes constraint logic metaprogramming whereby multiple computations $A_i$ each have a forgetful interpretation to a joint computation $J$, and a concrete computation $C$ is sought that simultaneously implements all of them (and makes the diagram commute). In general the tower is not a linear total order, but an arbitrary category, where developers may focus on some aspects and ignore others depending on the level of abstraction at which appear the issues they are battling with.

And now this semantic tower can be explored and modified at runtime, explicitly by the user, or implicitly by his software proxies.

4 Runtime Reflection

4.1 Migration

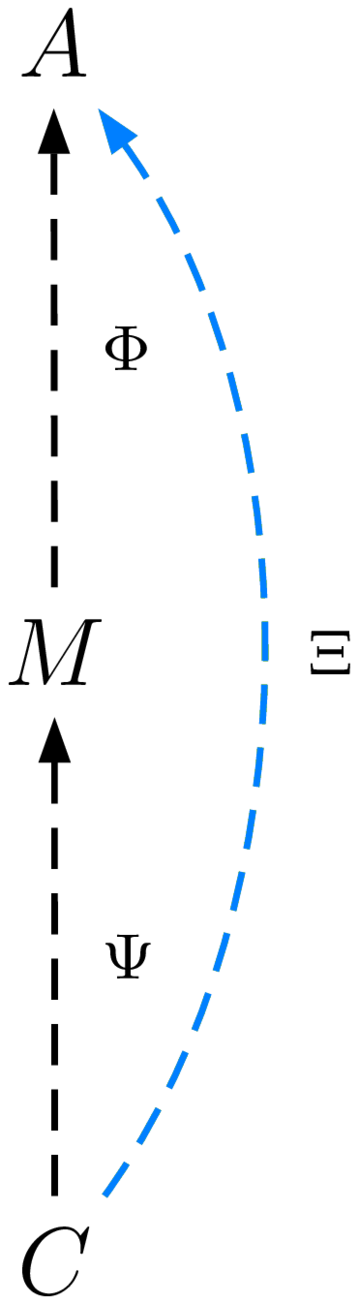
Our reflective protocol trivializes the notion of code migration: a given abstract computation $A$ can be implemented with a computation $C$ with an interpretation Φ; and if Φ is observable, then $C$ can be interrupted, an abstract state can be retrieved from its concrete state, and that state can be re-implemented with another computation $K$ with an interpretation Ψ, from which the computation resumes with all its dynamic state. Of course, any intermediate representation of states of $A$ can hopefully be optimized away when compiling $\Psi^{-1}\circ\Phi$; but as a fallback, it is trivial to implement this migration naïvely.

Many existing phenomena can be seen as migration: obviously, moving processes from one computer to another while it is running; which given a high-level language can now be done despite very different hardware architectures, without introducing some slow common virtual machine. But Garbage Collection can also be seen as a change in the representation of an abstract graph using addressed memory cells. Process synchronization can be seen as observing a collection of two (or more) processes as a shared abstract computation then switching back to a concrete view after effecting the high-level communication. Zero-copy routing can be seen as changing the interpretation function regarding who owns the buffers and what they mean, without copying any bits. JIT compilation, software upgrade (including database schema upgrade), dynamic refactoring, can be viewed as migration.

Our conceptual framework will hopefully make it easier to develop these difficult transformations in a provably correct way, and to automate migration, refactoring, upgrade, optimization, etc., of server processes without loss of service or corruption of data, when the short useful life of the underlying software and hardware stacks is all too predictable.

Interacting with software is usually limited to adding semantic layers on top of a rigid semantic tower provided to the users — through I/O, configuration, sometimes involving translating front-ends. In its general form, migration consists in interacting with software by changing semantic layers below. Migration is not limited to changes “at the bottom”, by adding one virtualization layer; it can happen at any intermediate level, by adding, removing, modifying any implementation layer (or slice of consecutive layers) anywhere, discarding the entire bottom of the tower if needs be — all while the software is running, without losing dynamic state.

4.2 Natural Transformations

Code instrumentation, tracing, logging, profiling, single-stepping, omniscient (time-travel) debugging, code and data coverage, access control, concurrency control, optimistic evaluation, orthogonal persistence, virtualization, macro-expansion, etc., are useful development tools that usually are written at great cost in an ad hoc way. They then have to be re-implemented for every semantic tower; and most of them are effectively lost in most cases when adding a semantic layer on top, at the bottom or in between. Developers thus have good tooling only as long as the issues they face happen at the abstraction level supported by their development system; if they happen at a higher or lower level, the quality of their tooling quickly drops back to zero.

We conjecture that all these techniques can be seen as natural transformations of implementations. In layman terms, this means that they can be written in a generic way that uniformly applies to all implementations that expose suitable variants of our first-class implementation protocol. They can then be made automatically available to all computations developed using our formalism, and preserved when arbitrarily adding, removing or recomposing semantic layers.

Therefore, a developer could start a program, notice some weird behavior when some conditions happen, enable time-travel debugging to explain the behavior, zoom into lower levels of abstraction if needed, or out of them if possible, and locate the bug — all while the program is running, with a guarantee that observing the program does not modify its behavior. Similarly, orthogonal persistence could be provided efficiently by default to all computations, without developers being required to add special hooks; and users could modify the parameters of their computations including persistence as their needs change or the market for cloud providers evolves — all of that at runtime without losing data.

5 Reflective Architecture

5.1 First-Class Semantic Tower

To take full advantage of our approach, we envision a system where all layers extend our first-class implementation protocol. Not only must programming languages or their libraries provide suitable primitives — all interactive systems, whether Emacs, some integrated development environment, some operating system shell, some distributed middleware, or even operating system API, etc., must also provide dynamic access to this protocol, or be wrapped in an abstraction that does.

At runtime, the system will maintain for every computation a first-class semantic tower: a category of abstraction levels to which the computation may be migrated. In that category are distinguished (1) the topmost computation that is being computed, that is fixed, specifies the desired semantics of the tower, and limits the access rights of all implementations, (2) and the bottommost computation that currently implements the above, that can be arbitrarily changed within those access rights, and (3) between the two (and optionally also above the former), the “current tower” of levels into which the current implementation can be interpreted without the need to migrate.

Now, it is usually desirable for migration to happen automatically as directed by an external program, rather than to be manually triggered by the user, or to follow a hardwired heuristic. The user could not care less about most details that migration deals about, whether managing cache lines, representing JIT code or data, or tracking availability of cloud resources; and a heuristic hardwired in the computation would make that computation both more complex and more rigid than necessary. Thus, every computation has its controller that can dynamically interact with the implementation and incrementally or totally migrate it, based on whatever signals are relevant.

Actually, the bottommost computation of a semantic tower is itself the topmost computation of another tower (with that tower becoming trivial when the topmost computation hits the “bare metal”). Thus there is a tower of controllers, that follows a tower of distinguished current implementations; and the controllers are themselves pretty arbitrary computations, with their own towers, etc. All these “slices” of a computation may or may not be handled by the same party; the end-user, application writer, compiler vendor, cloud provider, hardware designer, and many more, are each responsible for their slice of computation, constrained to implement the upper level with the lower one.

5.2 Performance and Robustness

Factoring a computation not just “horizontally” in “vertical” modules of functionality, but also “vertically” in “horizontal” implementation slices, is, we believe, a powerful paradigm for organizing software. It promises simpler software, with less development effort, more code reuse, easier proofs of correctness, better defined access rights, and more performance.

For instance, a computation generating video and sound can be well separated from the software that plays it to the user. This separation also enables I/O redirection without the application even having to know about it: the application can keep generating video and sound, oblivious to where they are output; the user can seamlessly redirect the output from one device to the input of another, or broadcast it to an adjustable set of devices, while the computation is running. From the point of view of the application, I/O effects are system calls into an outside program, the controller, that handles all requests, drastically simplifying the application (in categorical terms, effects are a free monad).

There is obviously a cost in maintaining a semantic tower and a controller for every computation; but there is also a performance benefit, directly related to the semantic simplification: implementations can directly bang bits to the proper devices or otherwise directly communicate with each other or inline calls, and there needs be no extra copying, marshalling, context-switching, or sources of slowness and high latency. Indeed, data routing, access control, code and data versioning and upgrade, etc., can now be resolved at a combination of compile-time and link-time, that can happen dynamically when the implementation is migrated, taking all dynamic data (including access rights, available formats, etc.) into account. Low-level code can be generated after protocol negotiation and environmental bindings, rather being generated before and then have to go through indirections or conditional dispatch at every access. In many cases, a lot of work can be eschewed that is not needed in the current configuration: for instance, video need not even be fully decoded or frames generated for a window that is not exposed, or music played when the sound is muted; yet the moment that the controller migrates the computation back to being visible or audible, these will be generated again — without the application programmer having to explicitly take these cases into consideration.

Beyond performance, robustness also benefits from the reflective factoring of computations into slices: applications can contain much less code, and their correctness and security properties are potentially much easier to tighten, enforce and verify, compared to traditional systems. Controllers that handle, e.g., video output, may remain relatively big and hard to ensure the robustness of — but they can still be smaller and easier to ascertain when broken into independent controllers than combined as libraries into a big program with a combinatorial explosion of potential interactions. Also there need not be the performance penalty of a runtime interpreter running as a server in a separate process.

5.3 Social Architecture

The main benefit we envision for a reflective architecture is in how it enables a different social organization of users and developers, around more modular software.

Without reflection, a developer writes an “application” that provides the entire semantic tower from the user-visible top to the “bottom” provided by the operating system. Virtualizing that bottom and doing something with it, while possible, takes advanced system administration skills. Not having resources to manage (much less develop and debug) the combinatorial explosion of potential implementation effects that users may desire, application developers can but offer sensible defaults for the majority of their users, and limited configuration for slightly more advanced users.

With reflection, there is no more fixed bottom for software. All software by construction runs virtualized, just not at the CPU level, but instead at the level of whatever language it is written in, under control of its controller. Developers do not have to care about persistence and other “non-functional requirements” (so-called), and users do not have to be frustrated because their requirements are not served by applications. Orthogonal persistence, infinite undo, time-travel, search, and all kinds of other services that can be implemented once as natural transformations are made available “for free” to all programs, under the control of the user, with an infinite variety of parameters (and sensible defaults), while developers do not have to care about any of the above.

We anticipate that with a reflective architecture, developers will have to write less code, of better quality and wider applicability, while users get to enjoy more functionality better adapted to their needs. Software will not be organized as “applications” but as “components”, that interact with each other more like Emacs packages or browser plugins, except with more principled ways of keeping software modular.

6 Conclusion and Future Work

The ideas presented in this paper remain largely unimplemented. Our most solid contribution so far are this trivial unifying formalism for programming language semantics, and the key notion of observability neglected in existing systems. The rest is prospective — but we hope that these prospects will inspire you to pursue this line of research. Our plan is to finish a larger document presenting these ideas, then to implement support for first-class implementations in Racket or some other Lisp system.

Bibliography