\settopmatter{printccs=true, printacmref=false, printfolios=false}

\author{François-René Rideau}

\affiliation{TUNES}

\email{fare@tunes.org}

\acmConference[OBT 2018]{Off the Beaten Track 2018}{January 13, 2018}{Los Angeles, California}

\copyrightyear{2018}

\setcopyright{none}

\acmDOI{}

\begin{CCSXML} <ccs2012> <concept> <concept_id>10003752.10010124.10010131.10010134</concept_id> <concept_desc>Theory of computation~Operational semantics</concept_desc> <concept_significance>500</concept_significance> </concept> <concept> <concept_id>10003752.10010124.10010131.10010137</concept_id> <concept_desc>Theory of computation~Categorical semantics</concept_desc> <concept_significance>500</concept_significance> </concept> <concept> <concept_id>10003752.10003753.10010622</concept_id> <concept_desc>Theory of computation~Abstract machines</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10003752.10003766.10003767.10003768</concept_id> <concept_desc>Theory of computation~Algebraic language theory</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10003752.10003766.10003767.10003769</concept_id> <concept_desc>Theory of computation~Rewrite systems</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10003752.10003790.10011119</concept_id> <concept_desc>Theory of computation~Abstraction</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10003752.10003790.10002990</concept_id> <concept_desc>Theory of computation~Logic and verification</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10003752.10003790.10003806</concept_id> <concept_desc>Theory of computation~Programming logic</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10003752.10003790.10011740</concept_id> <concept_desc>Theory of computation~Type theory</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10003752.10010124.10010138.10011119</concept_id> <concept_desc>Theory of computation~Abstraction</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10010940.10010941.10010942.10010944.10010946</concept_id> <concept_desc>Software and its engineering~Reflective middleware</concept_desc> <concept_significance>500</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011041.10011048</concept_id> <concept_desc>Software and its engineering~Runtime environments</concept_desc> <concept_significance>500</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011039.10011311</concept_id> <concept_desc>Software and its engineering~Semantics</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011041.10011044</concept_id> <concept_desc>Software and its engineering~Just-in-time compilers</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011041.10011045</concept_id> <concept_desc>Software and its engineering~Dynamic compilers</concept_desc> <concept_significance>300</concept_significance> </concept> <concept> <concept_id>10011007.10010940.10010941.10010949</concept_id> <concept_desc>Software and its engineering~Operating systems</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10010940.10010992</concept_id> <concept_desc>Software and its engineering~Software functional properties</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10010940.10011003</concept_id> <concept_desc>Software and its engineering~Extra-functional properties</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011050.10011017</concept_id> <concept_desc>Software and its engineering~Domain specific languages</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011050.10011055</concept_id> <concept_desc>Software and its engineering~Macro languages</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10011006.10011072</concept_id> <concept_desc>Software and its engineering~Software libraries and repositories</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10011074.10011111.10011113</concept_id> <concept_desc>Software and its engineering~Software evolution</concept_desc> <concept_significance>100</concept_significance> </concept> <concept> <concept_id>10011007.10011074.10011134</concept_id> <concept_desc>Software and its engineering~Collaboration in software development</concept_desc> <concept_significance>100</concept_significance> </concept> </ccs2012> \end{CCSXML}

\ccsdesc[500]{Theory of computation~Operational semantics}

\ccsdesc[500]{Theory of computation~Categorical semantics}

\ccsdesc[100]{Theory of computation~Type theory}

\ccsdesc[500]{Software and its engineering~Reflective middleware}

\ccsdesc[500]{Software and its engineering~Runtime environments}

\ccsdesc[300]{Software and its engineering~Just-in-time compilers}

\keywords{First-class, implementation, reflection, semantics, tower}

\begin{abstract} Software exists at multiple levels of abstraction, where each more concrete level is an implementation of the more abstract level above, in a semantic tower of compilers and/or interpreters. First-class implementations are a reflection protocol to navigate this tower at runtime: they enable changing the underlying implementation of a computation while it is running. Key is a generalized notion of safe points that enable observing a computation at a higher-level than that at which it runs, and therefore to climb up the semantic tower, when at runtime most existing systems only ever allow but to go further down. The protocol was obtained by extracting the computational content of a formal specification for implementations and some of their properties. This approach reconciles two heretofore mutually exclusive fields: Semantics and Runtime Reflection. \end{abstract}

Climbing Up the Semantic Tower — at Runtime

1 Introduction

Semantics predicts properties of computations without running them. Runtime Reflection allows unpredictable modifications to running computations. The two seem opposite, and those who practice one tend to ignore or prohibit the other. This work reconciles them: semantics can specify what computations do, reflection can control how they do it.

2 Formalizing Implementations

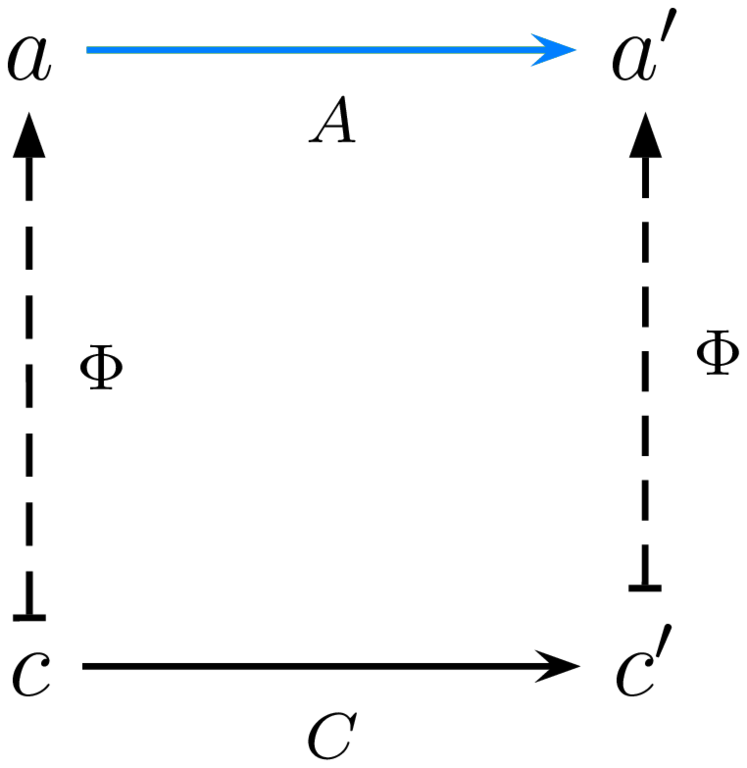
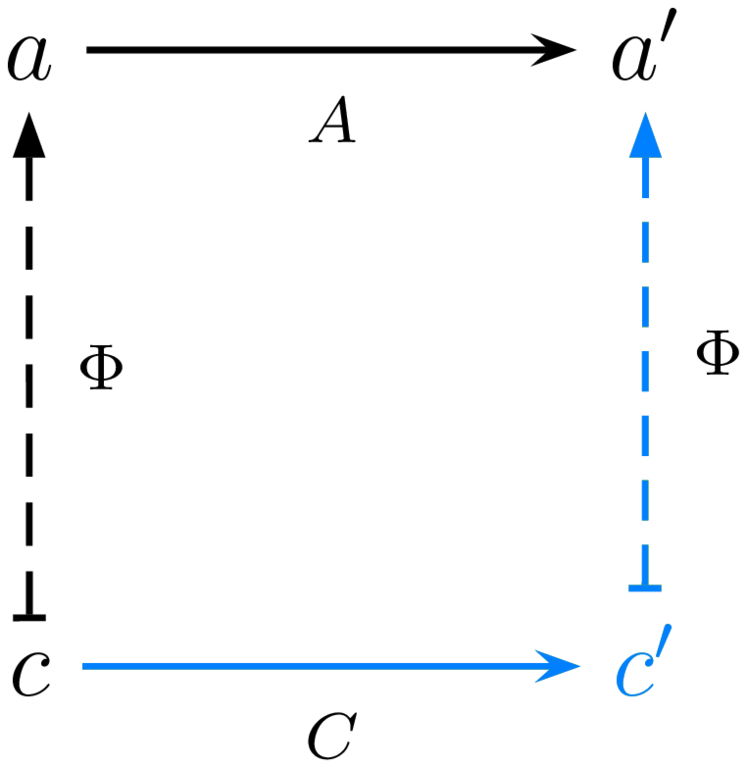
An elementary use of Category Theory can unify Operational Semantics and other common model of computations: potential states of a computation and labelled transitions between them are the nodes (“objects”) and arrows (“morphisms”) of a category. The implementation of an abstract computation $A$ with a concrete one $C$ is then a “partial functor” from $C$ to $A$, i.e. given a subset $O$ of “observable” safe points in $C$, a span of an interpretation functor from $O$ to $A$ and the full embedding of $O$ in $C$. Partiality is essential: concepts atomic in an abstract calculus usually are not in a more concrete calculus; concrete computations thus include many intermediate steps not immediately meaningful in the abstract.For instance, languages in the ALGOL tradition have no notion of explicit data registers or stacks, yet are typically implemented using lower-level machines (virtual or “real”) that do; meanwhile their high-level “primitives” each require many low-level instructions to implement.

Sound		Complete		Live		Observable

Figure 1: Some properties for implementations to have or not

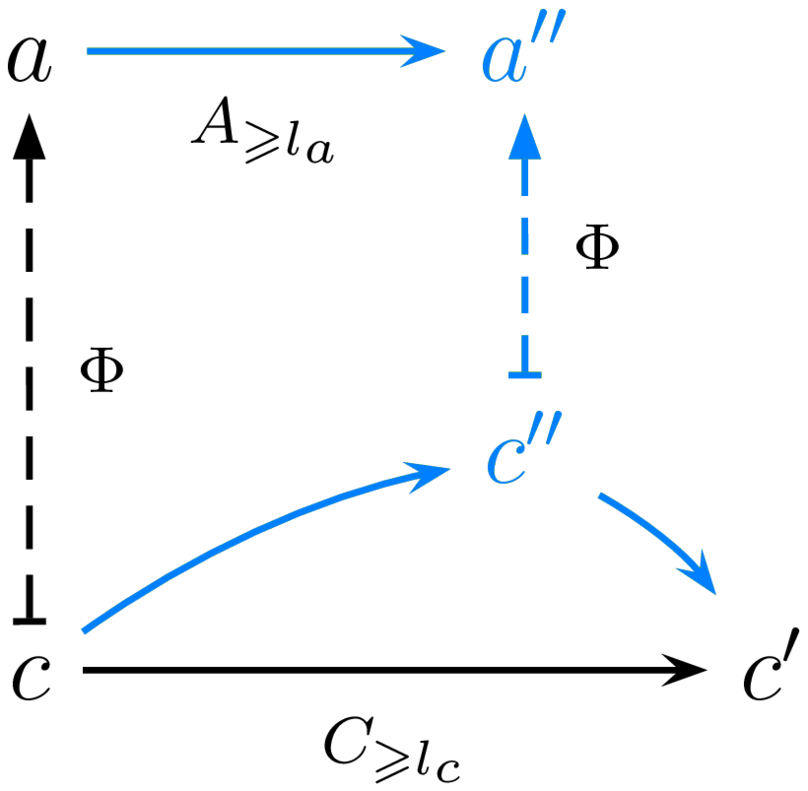
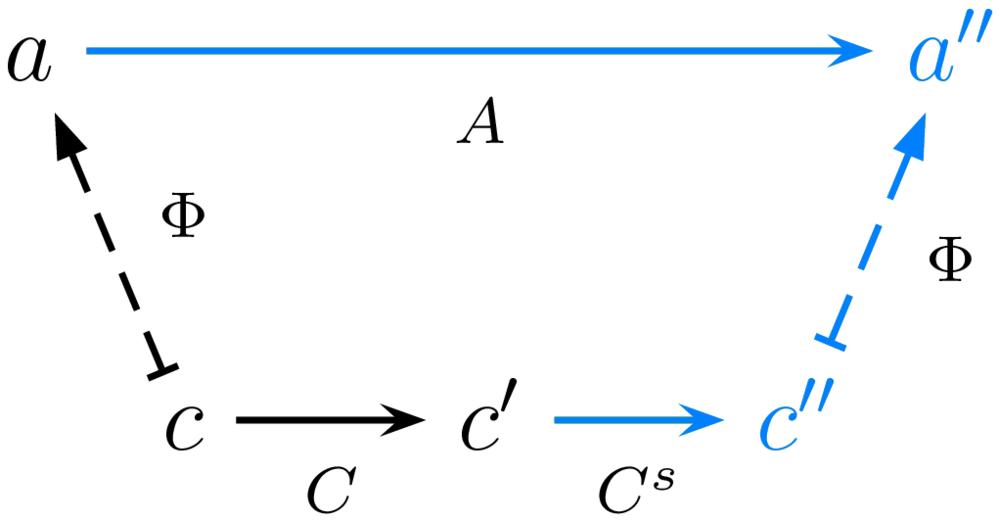
The mandatory soundness criterion is, remarkably, the same as functoriality. Many other interesting properties may or may not be hold for a given implementation: variants of completeness guarantee that abstract nodes or arrows are not left unimplemented in the concrete (e.g. can express the notion of simulation [4]); variants of liveness guarantee that progress in the abstract is made given enough progress in the concrete (e.g. can express “real time” behavior); and variants of observability guarantee that an observable abstract state can be recovered given any intermediate state at which the concrete computation is interrupted. These properties can be visualized using bicolor diagrams such as in figure 1.In these diagrams, computation is from left to right; abstract is above and concrete below; property premises are in black and conclusions in blue; and all diagrams commute. While an implementation is notionally from abstract to concrete, the opposite arrows of Abstract Interpretation are drawn, because functoriality goes from concrete to abstract, which is what matters when diagrams commute; for more details on the diagrams see [6].

3 Extracting a Runtime Protocol

Similarly, the computational content of completeness is a function that allows to control the concrete computation as if it were the abstract computation. The computational content of liveness is a function that advances the concrete computation enough to advance the abstract computation. All these functions and more form an API that allows arbitrary implementations of arbitrary languages to be treated as first-class objects, usable and composable at runtime.

4 Simulating or Performing Effects

Traditional reflection protocols [7] offer interfaces where only state can be reified, and effects always happen as ambient side-effects, except sometimes for limited ad hoc ways to catch them. By contrast, when extracting a protocol from a categorical specification, it becomes obvious that effects too deserve first-class reification, being the arrows of the reified computation category.

One simple way of reifying effects is as a journal recording I/O that happened during the computation — or would happen were the computation to actually run (or run again). More abstract representations can be symbolic, at a higher-level than a low-level logger could record; they could be monadic functions or arbitrary Kliesli arrows. In the end, there are two complementary approaches in which effects are either simulated or performed. Two functions simulate and perform may translate one approach into the other: but while perform can be written on top of any expressive enough system (at a cost), achieving simulate requires rewriting the entire system if the existing implementation does not offer a suitable reflection protocol.

Now the reflection protocol itself includes effects beyond those of the computations being reified and reflected — if only partiality and its dual non-determinism. Implementations and interpretations are partial and may fail on some nodes or arrows. And even if a computation is itself deterministic or at least confluent, running or advancing it includes non-determinism as to how much work will be done according to what evaluation strategy. A logical specification of the protocol must therefore expose these effects.

5 Applications

The protocol, thanks to its crucial notion of observability, enables navigating up and down a computation’s semantic tower while it is running. Developers can then zoom in and out of levels of abstraction and focus their tools on the right level for whatever issue is at hand, neither too high nor too low. Computations can be migrated from one underlying implementation to the other, one machine or configuration to the other — changing a running engine. Recovering an abstractly observable safe point also enables safely killing threads and upgrading code, thus achieving a robustness that only Erlang [8] can currently provide. Code instrumentations can be seen as the categorical opposites of Natural Transformations; they can be written in a generic way, added to running code, configured independently from code; they can provide orthogonal persistence, access control, time-travel debugging, and other capabilities to all languages. etc.

Each of these applications has been done before, but in heroic ways, available only to one implementation of one language, using some ad hoc notion of safe points (PCLSRing [1], Garbage Collection [9], etc.). The promise of this runtime reflection protocol is to achieve these applications in comparatively simple yet general ways, and made available universally: tools such as shells, debuggers, or code instrumentations, can then work on all possible implementations of all languages, specialized using e.g. typeclasses.

Finally, rooting a reflection protocol in formal methods means it is now possible reason about metaprograms, and maybe even feasably prove them correct; they need no longer invalidate semantic reasoning nor introduce unmanageable complexity.

6 Conclusion and Future Work

The ideas above remain largely unimplemented. But they already provide a new and promising way of looking at either the semantics of implementations or the design of reflection protocols — and more importantly, at the synergy between those two estranged fields. My plan is to further implement the protocol in Gambit Scheme: it already implements observability and migration at the level of its GVM [2], and there is a Racket-like module system called Gerbil to develop closed languages on top of it.

See my presentation at https://youtu.be/heU8NyX5Hus.

Bibliography